The Stack

There are really two opposite ways to be stuck on a logic puzzle. The more usual way is to be unable to eliminate possibilities, so that the number of solutions under consideration is too large to simply iterate through. The other way is to eliminate all the possibilities. If you can do that, and the puzzle actually does have a solution, it means there’s an error in your reasoning somewhere, a variation that you’re forgetting about. But knowing that there’s an error doesn’t help much in finding it.

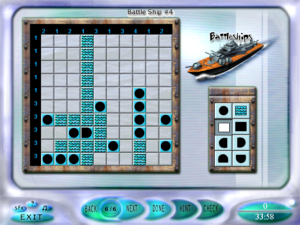
That’s the position I’m in with the last Battleships puzzle. There’s one four-long ship in every puzzle, and this puzzle has only one row or column that can hold it. Since the grid is 10×10, that means there are only seven positions this ship can go in. And I can prove every single one impossible.

There must be a mistake. That much is clear. But is the mistake mine or theirs? I actually think it’s probably mine in this instance. Battleships has a certain amount of error-detection built in. There are exactly 20 tiles worth of ships in every grid, so you can tell if there’s a mistake in one of the row or column numbers by adding them all up and seeing if you get 20. This would fail if there are two or more errors that cancel each other out perfectly, but how likely is that? So I think I’ll have to keep on looking for a solution here.

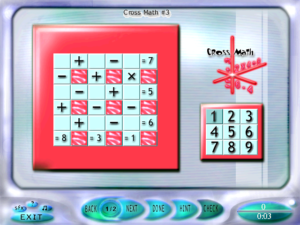I can’t say the same for the last remaining Cross Math puzzle. Here, a similar summing technique proved that the puzzle is wrong. In these puzzles, you have to fill the numbers 1 through 9 in such a way to satisfy all six horizontal and vertical equations. Now, observe that the horizontal equations in this one have no multiplication or division. If they had nothing but addition, then the sum of all three rows would have to add up to the sum of all the numbers from 1 through 9, which is to say, 45. But some of the numbers are subtracted. The effect of subtracting a number instead of adding it is to subtract that number from the total sum twice: once for removing it as an addend, and once for the actual subtraction. So no matter what numbers have their signs flipped, the result will differ from 45 by an even number. The sum of all three rows therefore has to be odd. But this puzzle gives us rows that sum to 18.

Having thus convinced myself that at least one of the sums here was wrong, I told the game that I was done with the puzzle, and was pleased to be vindicated: in the game’s solution, the top row makes 8, not the 7 claimed. Proving a puzzle incorrect in this way is a sort of metapuzzle, and at least as satisfying as solving the puzzle itself.