The Stack

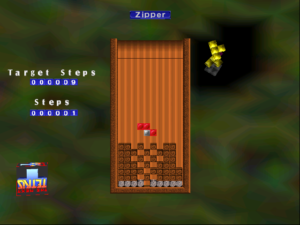OK, let’s try to analyze this a little. The Next Tetris practice level 19, “Zipper”, has the initial layout pictured here. There are seven rows of garbage squares. Only the bottommost row — the grey one — counts for completing the level, but the gap in that row can only be accessed by fist getting rid of the row above it, which in turn needs the row above that deleted, and so on. The level is supposed to be completed in nine moves, which means adding 36 squares to the board. There are 18 empty spaces, which leaves 18 squares to lump up on top. The board is 10 squares wide, so at most one additional row above the initial garbage can be filled, leaving 8 squares left at the end. One of the big questions here is whether it’s worthwhile to try to complete such an extra row.

Here are the nine pieces, in the order they appear:

(Recall that color is significant. Blocks of the same color fuse together and fall as a unit, while a piece composed of multiple colors will break apart upon first coming to rest. This has some non-obvious consequences. For example, if you drop the first piece here the opposite way up into one of the gaps on this board, it’ll stay the shape it is until you delete the first row, at which point the right side will fall one row farther than the left side, and the red squares on both sides will stick together, forming a unit two squares wide.)

Now, all of the gaps in the initial layout are one square wide. Of the 36 squares that compose our nine pieces, 11 have a horizontal neighbor of the same color no matter how they’re rotated, and thus cannot possibly fit into a one-square-wide gap. Let’s call these “blocker squares”. Another 11 squares are directly attached to blocker squares of the same color. If these are placed in a gap, the adjacent blocker square will have to be above it, preventing access to any further gaps in that column, unless you can complete that extra row and delete it. The remaining 14 squares are detached units or straght columns that can be used to freely fill in whatever needs them, provided they don’t glob onto something else of the same color and get stuck.

The obvious thing to do with the straight piece (or “I” piece) is to put it in the 4-deep straight hole on the right. But obviousness is no guarantee of correctness — the I could also very well fill the vertically-arranged four gaps in the very middle. This works well with the level’s name — the I is like the zipper that pulls downward through the middle and tears the whole structure apart. Also, the I is a color that isn’t used in any of the other pieces, which makes it more useful in the middle, where it helps to keep things from getting stuck to each other. But if you put it there, you’ll have to come up with some other way to fill in the straight gap, and nothing else fits quite as easily. Filling an extra row is almost necessary in such a scheme.

Two other pieces are of special note. The 2-by-2 block (or “O”) is composed entirely of blocker squares, and is of no use whatever for filling gaps in the garbage. It’s also composed of a color almost unused otherwise, so it isn’t much use as a complication either: just throw it to the side and it won’t interfere. This makes me think that it serves in the puzzle to help complete the extra row. At this point, there’s so much circumstantial evidence in favor of the extra row hypothesis that I’ll be really surprised if it’s wrong.

The other is the final piece, the green “S”. Because it’s the last piece, it has to either fill in the final gap, or trigger a cascade that fills it in. On purely aesthetic grounds, I suspect that a final cascade won’t involve only part of the initial layout. Either the garbage above the goal row will all be gone by the time this piece is placed, or it’ll all still be there. In the latter case, there’s some difficulty in placing the S. This scenario requires all but one of the gappy columns to be capped with a tower of pieces waiting to fall into place. The only original gap that could possibly accommodate the S in this situation is the straight pit on the right, which would have to have three pieces in it already and have nothing on its left to keep the S out; this could clearly only happen if an extra row had been deleted. Alternately, the S itself could complete the extra row.

So, I’m coming to the conclusion that there’s probably an extra row to be built and deleted, and the I could plausibly go in the middle. I’ll have to try things along these lines the next time I play.